
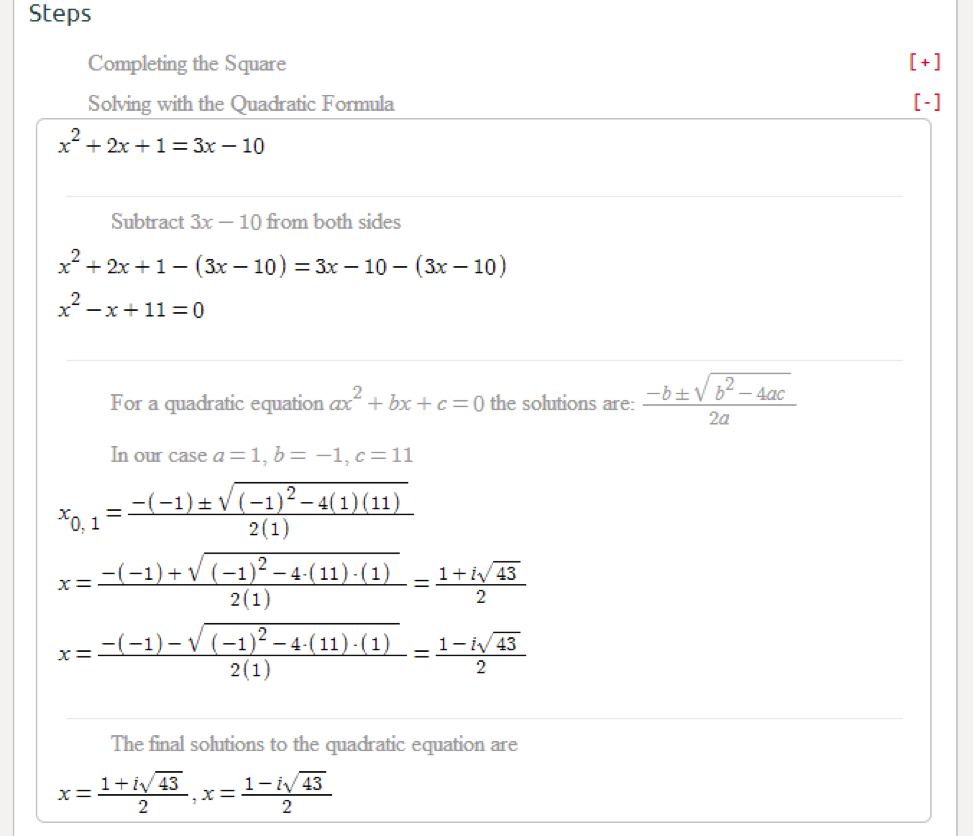
Just as in the previous example, the x-intercepts match the zeroes from the Quadratic Formula. Reinforcing the concept: Compare the solutions we found above for the equation 2 x 2 − 4 x − 3 = 0 with the x-intercepts of the graph: But unless you have a good reason to think that the answer is supposed to be a rounded answer, always go with the exact form. If you're wanting to graph the x-intercepts or needing to simplify the final answer in a word problem to be of a practical ("real world") form, then you can use the calculator's approximation. In the example above, the exact form is the one with the square roots of ten in it. You can use the rounded form when graphing (if necessary), but "the answer(s)" from the Quadratic Formula should be written out in the (often messy) "exact" form. Step 1: calculate the discriminant, using the formula: b24ac.
#Quadratic formula calculator with steps how to#
Using this online calculator, you will receive a detailed step-by-step solution to your. In this section we learn how to solve quadratic equations. In general, no, you really shouldn't the "solution" or "roots" or "zeroes" of a quadratic are usually required to be in the "exact" form of the answer. This online calculator will help you to solve quadratic equation. So long as a 0 a 0, you should be able to factor the quadratic equation. You may also see the standard form called a general quadratic equation, or the general form. Consider a quadratic equation in standard form: ax2 + bx + c 0 a x 2 + b x + c 0. A quadratic equation always has the form ax2 + bx + c 0 with a 0. The quadratic formula is used to solve quadratic equations. Can I round my answers from the Quadratic Formula? Step 3: Reminder for the Quadratic Equations. Quadratic Formula Calculator The calculator below solves the quadratic equation of ax 2 + bx + c 0. Then the answer is x = −0.58, x = 2.58, rounded to two decimal places. The quadratic equation ( y ax2 + bx + c ) is equal to ( y ax2 + bx ), because the constant term ‘c’ does not affect the parabola. Trust me on this! What is an example of using the Quadratic Formula? The quadratic equation of parabola: Y ax2 + bx + c where (a, b) is the co-efficient at x and ‘c’ is a constant term. In other words, don't be sloppy and don't try to take shortcuts, because it will only hurt you in the long run. Remember that " b 2" means "the square of ALL of b, including its sign", so don't leave b 2 being negative, even if b is negative, because the square of a negative is a positive. Make sure that you are careful not to drop the square root or the "plus/minus" in the middle of your calculations, or I can guarantee that you will forget to "put them back in" on your test, and you'll mess yourself up. And it's a " 2 a" under there, not just a plain " 2". Pull out the numerical parts of each of these terms, which are the " a", " b", and " c" of the Formula.Īdvisories: The " 2 a" in the denominator of the Formula is underneath everything above, not just the square root. Arrange your equation into the form "(quadratic) = 0".Īrrange the terms in the (equation) in decreasing order (so squared term first, then the x-term, and finally the linear term).


 0 kommentar(er)
0 kommentar(er)
